Delving into the world of mathematical competitions, numerous PDF collections, like Kapur’s “1000 Mathematical Challenges” and Holton’s guide,
offer invaluable practice. These resources, containing challenging problems from INMO, RMO, and international olympiads,
are designed to sharpen problem-solving skills and deepen mathematical understanding for aspiring contestants.
Accessing these PDFs provides a foundation for success, supplementing learning with diverse problem sets and advanced techniques.
What are Mathematical Olympiads?
Mathematical Olympiads are prestigious competitions designed to challenge and inspire mathematically gifted students. They extend far beyond standard curriculum, focusing on creative problem-solving and logical reasoning. Resources like the “1000 Mathematical Challenges” PDF by J.N. Kapur showcase the type of problems encountered – often drawn from the Indian National Mathematical Olympiad (INMO) and Regional Mathematical Olympiad (RMO), alongside problems from Singapore, Israel, and Portugal.
These Olympiads aren’t simply about memorizing formulas; they demand a deep understanding of mathematical concepts. Derek Allan Holton’s “A First Step To Mathematical Olympiad Problems” emphasizes this, focusing on problem-solving techniques across areas like combinatorics and number theory. PDF collections serve as vital training grounds, exposing students to the breadth and depth of Olympiad-level mathematics, preparing them for rigorous competition and fostering a love for the subject.
Participation cultivates analytical skills and a strategic approach to problem-solving.
Importance of Solving Olympiad Problems
Engaging with Olympiad problems, particularly through resources like the “1000 Mathematical Challenges” PDF, offers benefits extending beyond competition success. Solving these problems cultivates critical thinking, logical reasoning, and a persistent approach to challenges. The diverse problem sets – encompassing INMO, RMO, and international contests – demand a flexible and adaptable mindset.
Working through these PDFs isn’t just about finding solutions; it’s about understanding the why behind them. Holton’s “A First Step…” highlights the importance of mastering problem-solving techniques. Exposure to varied problem types, like those found in multi-part collections, builds a strong mathematical foundation. Furthermore, studying approaches used in the Chinese Mathematical Olympiad, as seen in available PDFs, provides valuable insights into effective strategies and innovative thinking.
Consistent practice is key to unlocking mathematical potential.
Target Audience for 1000 Mathematical Olympiad Problems PDFs
PDF collections like J.N. Kapur’s “1000 Mathematical Challenges” and Derek Holton’s “A First Step…” cater to a broad spectrum of mathematical enthusiasts. Primarily, these resources are invaluable for students preparing for mathematical olympiads – specifically, those aiming for INMO and RMO levels. However, the audience extends beyond competitors.
School students with a keen interest in mathematics, seeking to deepen their understanding and challenge themselves, will find these PDFs highly beneficial. Coaches and instructors of mathematical competitions also represent a key target group, utilizing the problems for training and curriculum development. The inclusion of problems from Singapore, Israel, and Portugal broadens the appeal to an international audience.
Essentially, anyone passionate about mathematical problem-solving can benefit from these resources.

Key Resources: Popular PDF Collections
Essential PDF resources include J;N. Kapur’s extensive “1000 Mathematical Challenges” and Derek Allan Holton’s “A First Step,” offering diverse problems and techniques.
J.N. Kapur’s “1000 Mathematical Challenges”
J.N. Kapur’s “1000 Mathematical Challenges” is a cornerstone resource for aspiring Olympiad participants. This comprehensive PDF collection meticulously compiles problems from the Indian National Mathematical Olympiad (INMO) spanning 1986-1995, and the Regional Mathematical Olympiad (RMO) from 1990-1995.
However, its scope extends beyond Indian competitions, incorporating challenging problems sourced from international olympiads held in Singapore, Israel, and Portugal. This broad inclusion provides a diverse range of problem-solving experiences. The book isn’t merely a problem set; it offers detailed solutions, enabling self-study and a deeper understanding of the underlying mathematical principles.
It’s a valuable asset for students preparing for competitive exams and seeking to enhance their mathematical prowess. The resource is often available as a free download in PDF format.
Coverage: INMO & RMO Problems (1986-1995)
J.N. Kapur’s “1000 Mathematical Challenges” provides extensive coverage of problems featured in the Indian National Mathematical Olympiad (INMO) and the Regional Mathematical Olympiad (RMO) between 1986 and 1995. This ten-year span represents a significant archive of challenging mathematical questions specifically designed to test problem-solving abilities.
The collection’s focus on these two prominent Indian olympiads makes it an ideal resource for students preparing for similar competitions. It allows for targeted practice with problems mirroring the style and difficulty level encountered in these exams.
Students can analyze past papers, identify recurring themes, and refine their techniques. The PDF format facilitates easy access and efficient study, making it a cornerstone for Indian Olympiad preparation.
Inclusion of International Problems (Singapore, Israel, Portugal)
Expanding beyond the Indian Olympiad landscape, J.N. Kapur’s “1000 Mathematical Challenges” enriches its collection with problems sourced from international mathematical competitions. Specifically, the PDF incorporates challenges from Singapore, Israel, and Portugal, offering a broader perspective on Olympiad-level mathematics.
This international inclusion is invaluable for students aiming to compete on a global stage. Exposure to diverse problem-solving approaches and mathematical styles cultivates adaptability and enhances critical thinking.
The inclusion of these problems allows students to benchmark their skills against international standards and prepare for the nuances of different competition formats. It’s a testament to the book’s comprehensive approach to mathematical Olympiad preparation.
Derek Allan Holton’s “A First Step To Mathematical Olympiad Problems”
Complementing extensive collections like Kapur’s “1000 Mathematical Challenges”, Derek Allan Holton’s book provides a foundational approach to tackling Olympiad problems. Published by World Scientific in 2010, it’s readily available through the Internet Archive for download, borrowing, or streaming.
Holton’s work isn’t merely a problem set; it’s a guide for both students and instructors. It focuses on developing core problem-solving techniques, making it ideal for those new to the competitive landscape. The content covers essential areas like combinatorics, graph theory, number theory, and geometry.
This resource is particularly beneficial for building a strong conceptual understanding before diving into larger, more complex collections.
Focus on Problem-Solving Techniques
Derek Allan Holton’s “A First Step…” emphasizes mastering techniques before tackling vast problem sets like those found in Kapur’s “1000 Mathematical Challenges”. The book, available via the Internet Archive, doesn’t just present problems; it teaches how to approach them strategically.
A key element is the “Jugs and Stamps” method, a pedagogical approach to deconstructing complex problems into manageable steps. This fosters a systematic thinking process crucial for success in mathematical olympiads. The book guides readers through identifying key concepts, formulating plans, and executing solutions.
This focus on methodology is invaluable, enabling students to confidently navigate the challenges presented in larger PDF collections.
Topics Covered: Combinatorics, Graph Theory, Number Theory, Geometry
Derek Allan Holton’s “A First Step To Mathematical Olympiad Problems” systematically covers core areas frequently tested in competitions, mirroring the scope found within collections like J.N. Kapur’s “1000 Mathematical Challenges”. Combinatorics is explored through counting principles and arrangements, while Graph Theory introduces network analysis.
Number Theory, a cornerstone of olympiads, receives dedicated attention, alongside Geometry – encompassing Euclidean principles and constructions. Holton’s approach builds a strong foundation in these areas, preparing students for the diverse problems presented in the INMO and RMO problems included in Kapur’s compilation.
These PDFs offer extensive practice across these vital mathematical disciplines.

Core Mathematical Areas in Olympiad Problems
PDF resources, such as Kapur’s compilation, heavily emphasize Number Theory, Algebra, Geometry, and Combinatorics, providing extensive practice
and problem-solving strategies for aspiring olympiad participants.
Number Theory
Number Theory forms a cornerstone of many mathematical olympiad problems, and PDF collections like J.N. Kapur’s “1000 Mathematical Challenges” provide extensive coverage. These resources delve into Divisibility and Prime Numbers, exploring concepts crucial for solving complex problems.
Diophantine Equations, requiring integer solutions, are frequently featured, demanding both analytical and problem-solving skills. The problems sourced from INMO, RMO, Singapore, Israel, and Portuguese olympiads within these PDFs offer a diverse range of challenges.

Mastering these concepts is vital, as Number Theory often intersects with other areas like Algebra and Combinatorics, creating multi-faceted problems that test a contestant’s overall mathematical prowess. Consistent practice with these PDF materials is key to building a strong foundation.
Divisibility and Prime Numbers
Divisibility rules and prime number theory are foundational elements extensively covered within PDF collections like J.N. Kapur’s “1000 Mathematical Challenges”. These problems often require identifying prime factors, understanding modular arithmetic, and applying theorems related to divisibility.
Problems sourced from various olympiads – INMO, RMO, and international competitions – emphasize the practical application of these concepts. Expect challenges involving finding the greatest common divisor (GCD), least common multiple (LCM), and proving statements about prime numbers.
Mastering these fundamentals is crucial, as they frequently appear in more complex problems. Consistent practice with the diverse examples presented in these PDF resources will build a strong understanding and enhance problem-solving speed and accuracy.
Diophantine Equations
Diophantine equations, polynomial equations where only integer solutions are sought, represent a significant challenge within mathematical olympiads, and are well-represented in resources like Kapur’s “1000 Mathematical Challenges”. PDF collections often feature problems requiring clever manipulation and number theory insights to find these integer solutions.
Expect problems involving linear and quadratic Diophantine equations, alongside more complex forms demanding advanced techniques. These challenges frequently test a contestant’s ability to apply modular arithmetic, factorization, and other number-theoretic tools.
Consistent practice with these equation types, as provided by the PDFs, is vital for developing problem-solving intuition and mastering the necessary techniques. Successfully tackling these problems builds a strong foundation for more advanced mathematical concepts.
Algebra
Algebraic problem-solving forms a cornerstone of mathematical olympiads, and PDF resources like Kapur’s compilation and Holton’s “A First Step” provide extensive practice. These materials cover a broad spectrum of algebraic concepts, crucial for success in competitions.
Expect a focus on manipulating polynomials and solving equations, often requiring ingenious approaches beyond standard textbook methods. PDFs frequently include problems testing skills in factorization, root finding, and understanding polynomial identities.
Inequalities also feature prominently, demanding a grasp of AM-GM, Cauchy-Schwarz, and other powerful techniques. Mastering these algebraic tools, through dedicated practice with PDF problem sets, is essential for achieving high scores.
Polynomials and Equations
PDF collections, such as J.N. Kapur’s “1000 Mathematical Challenges,” dedicate significant portions to polynomials and equations. These problems often transcend routine algebraic manipulation, demanding creative problem-solving skills.
Expect to encounter problems involving finding roots of polynomials, often with constraints or requiring clever factorization techniques. PDFs frequently present equations that aren’t immediately solvable through standard methods, pushing you to explore alternative approaches like Vieta’s formulas.
Mastering polynomial identities and understanding the relationship between coefficients and roots are crucial. Holton’s guide also emphasizes these concepts. Consistent practice with these PDF resources builds the necessary intuition and proficiency for tackling complex olympiad-level questions.
Inequalities
Inequalities represent a cornerstone of mathematical olympiad problems, and PDF resources like Kapur’s compilation offer extensive practice in this area. These aren’t simply about finding greater or lesser values; they demand a deep understanding of mathematical principles.
Expect problems requiring the application of AM-GM, Cauchy-Schwarz, and other key inequalities. PDFs often present inequalities that necessitate clever manipulation and insightful application of these tools. Holton’s “A First Step…” emphasizes building a strong foundation in these techniques.
Developing the ability to recognize when and how to apply specific inequalities is vital. Consistent practice with these PDFs hones this skill, preparing you to tackle challenging olympiad questions effectively and efficiently.
Geometry
Geometry consistently features prominently in mathematical olympiads, and PDF collections like those by Kapur provide a wealth of problems to hone your skills. These aren’t limited to standard textbook geometry; expect challenges demanding creative problem-solving.
Focus areas include Euclidean geometry basics, angle chasing, and the application of theorems like Ceva’s and Menelaus’. Holton’s work specifically highlights geometric constructions and proofs as essential techniques. PDFs often present diagrams requiring careful analysis and strategic thinking.
Mastering geometric intuition and developing a systematic approach to problem-solving are crucial. Regular practice with these PDF resources builds confidence and prepares you for the complexities of olympiad-level geometry problems.
Euclidean Geometry Basics
A solid foundation in Euclidean geometry is paramount for tackling olympiad problems, and PDF collections like Kapur’s “1000 Mathematical Challenges” frequently revisit these fundamentals. Expect problems testing your knowledge of triangle congruence, similarity, and the properties of angles and lines.
Understanding circle theorems, polygon properties, and basic area formulas is essential. Holton’s “A First Step…” emphasizes building this base before moving to more complex concepts. PDFs often present problems requiring you to apply these basics in unconventional ways.
Mastering these fundamentals allows you to efficiently analyze diagrams and identify key relationships, forming the basis for more advanced geometric problem-solving. Consistent practice with PDF resources solidifies this crucial foundation.
Geometric Constructions and Theorems
Olympiad geometry often extends beyond basic theorems, demanding proficiency in constructions and a deep understanding of related theorems. PDF collections, such as those containing problems from the INMO and RMO featured in Kapur’s work, frequently include problems requiring geometric constructions using compass and straightedge.
Familiarity with theorems like Ceva’s, Menelaus’, and Ptolemy’s is crucial. Holton’s book likely introduces these, and PDFs provide ample opportunity to apply them. Expect problems where you must prove geometric relationships or find specific lengths and angles through clever constructions.
Developing spatial reasoning and the ability to visualize geometric transformations is key. Consistent practice with PDF problem sets will hone these skills, preparing you for challenging olympiad scenarios.
Combinatorics
Combinatorial problems are a staple of mathematical olympiads, frequently appearing in collections like J;N. Kapur’s “1000 Mathematical Challenges” and Holton’s “A First Step…”. These PDF resources offer extensive practice in counting techniques, essential for success.
Mastering fundamental principles like the addition and multiplication principles is vital. Expect problems involving permutations, combinations, and arrangements with constraints. PDFs will present scenarios requiring you to determine the number of ways to select, arrange, or partition objects.
Advanced topics like inclusion-exclusion and generating functions may also appear. Holton’s book specifically covers combinatorics, and consistent practice with PDF problem sets will build a strong foundation in this crucial area.
Counting Principles
Fundamental counting principles form the bedrock of combinatorial problem-solving, heavily featured within PDF collections like Kapur’s “1000 Mathematical Challenges”. These principles – addition, multiplication, and division – are consistently tested in olympiad settings.
The addition principle addresses mutually exclusive events, while the multiplication principle handles sequential choices. PDFs provide numerous exercises to solidify understanding of when and how to apply each. Expect problems requiring you to count possibilities, arrangements, and selections.
Practice with these principles is crucial, as they underpin more complex combinatorial techniques. Holton’s book also emphasizes these basics. Utilizing PDF problem sets allows for targeted practice and builds a strong foundation for tackling challenging olympiad questions.
Permutations and Combinations
Permutations and combinations are core topics within the combinatorial section of mathematical olympiads, extensively covered in resources like the “1000 Mathematical Challenges” PDF. Understanding the distinction – order matters in permutations, but not in combinations – is vital.
PDF collections offer a wealth of problems requiring the application of formulas (nPr and nCr) and logical reasoning to determine whether a permutation or combination is appropriate. Expect scenarios involving arrangements, selections, and groupings.
Holton’s “A First Step…” emphasizes problem-solving techniques applicable to these concepts. Mastering these techniques through consistent practice with PDF problem sets is key to success. These problems often require careful consideration of constraints and conditions.

Utilizing PDF Resources Effectively
Maximizing learning from PDFs like Kapur’s requires strategic problem-solving, consistent practice, and supplementing with online resources for enhanced understanding and skill development.
Strategies for Approaching Difficult Problems
Tackling challenging problems from resources like the “1000 Mathematical Challenges” PDF demands a systematic approach. Begin by thoroughly understanding the problem statement, identifying key concepts, and attempting simpler, related problems first. Break down complex problems into smaller, manageable parts, and explore different solution pathways.
Don’t be afraid to experiment with various techniques – drawing diagrams, working backwards, or considering special cases. If stuck, review similar solved problems for inspiration, but avoid directly copying solutions. Persistence is key; dedicate sufficient time and effort before seeking assistance.
Holton’s “A First Step” emphasizes problem-solving techniques, which are crucial here. Regularly review attempted problems, analyzing errors and refining your approach. Remember, the goal isn’t just finding the answer, but developing a deeper understanding of the underlying mathematical principles.
Importance of Practice and Review
Consistent practice with resources like the “1000 Mathematical Challenges” PDF is paramount for success in mathematical olympiads. Solving a large volume of problems, encompassing diverse areas like number theory and geometry, builds fluency and intuition. However, practice alone isn’t sufficient; thorough review is equally crucial.
Analyze solved problems, identifying patterns, common techniques, and areas for improvement. Revisit previously challenging problems after a period, attempting to solve them independently. This reinforces understanding and solidifies problem-solving skills.
Utilize the PDF collections as a continuous learning tool, not just a source of problems. Regular review helps retain knowledge and develop a deeper appreciation for the elegance and power of mathematical reasoning, mirroring the approach found in advanced problem sets.
Supplementing PDFs with Online Resources

While PDF collections like Kapur’s “1000 Mathematical Challenges” provide a strong foundation, online resources are invaluable supplements. Websites and forums dedicated to mathematical olympiads offer a wealth of additional problems, solutions, and discussions. Explore platforms like Art of Problem Solving (AoPS) for interactive learning and community support.
Utilize online resources to research specific topics encountered in the PDFs, deepening your understanding of concepts like combinatorics or Diophantine equations. Access past olympiad papers and solutions to broaden your exposure.
Combine PDF practice with online learning to create a comprehensive study plan, mirroring the strategies employed in Chinese Mathematical Olympiad approaches. This blended approach maximizes learning and enhances problem-solving abilities.

Advanced Problem Sets & Series
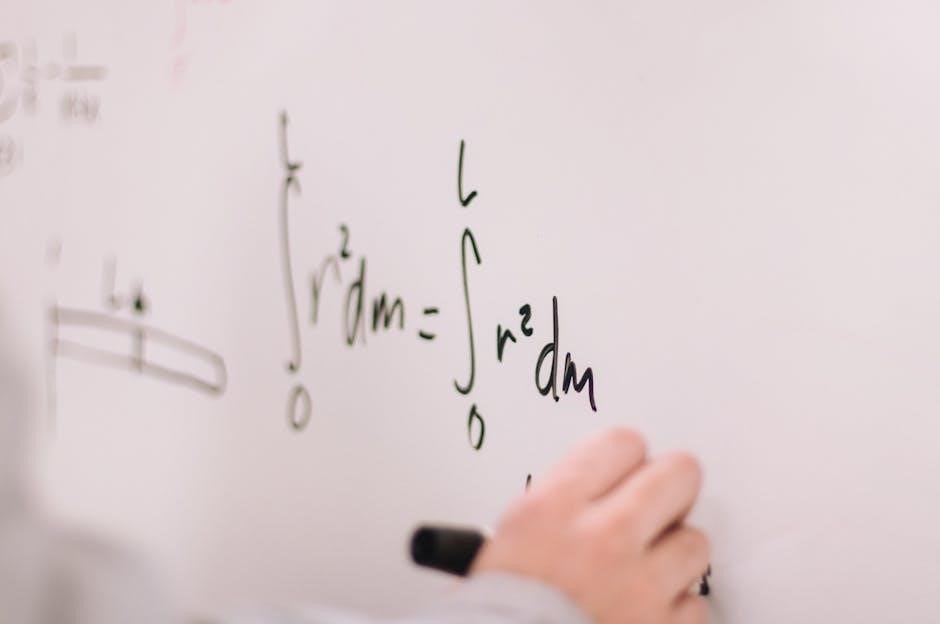
Beyond initial PDFs, explore multi-part collections and series, including those mirroring Chinese Olympiad strategies, to extend problem-solving skills and tackle complex challenges.
Continued practice is key!
Multi-Part Olympiad Problem Collections
Expanding beyond single PDF volumes, dedicated students often benefit from exploring multi-part Olympiad problem collections; These series, frequently originating from national competitions like the Chinese Mathematical Olympiad, offer a progressive learning curve. A four-part series, for example, systematically introduces increasingly complex problems, building upon foundational concepts.
Resources like those found on ResearchGate showcase this approach, providing curated sets designed to challenge and refine problem-solving abilities. While J.N. Kapur’s “1000 Mathematical Challenges” provides a substantial base, these extended collections offer further depth and breadth. They often emphasize a specific methodology, such as the Chinese approach to mathematical education, known for its rigor and focus on conceptual understanding.
These collections are invaluable for students aiming for advanced competition levels, providing exposure to a wider range of problem types and solution techniques. They complement initial PDF resources, fostering a more comprehensive and nuanced understanding of Olympiad mathematics.
Focus on Chinese Mathematical Olympiad Approaches
The Chinese Mathematical Olympiad (CMO) is renowned for its challenging problems and unique problem-solving techniques. Many advanced resources, including supplementary materials to collections like the “1000 Mathematical Challenges” PDF, delve into these approaches. These methods often emphasize a deep understanding of fundamental principles and creative problem manipulation.
Documents discussing the Chinese approach highlight a focus on rigorous proof-writing and a systematic exploration of possible solutions. This contrasts with purely computational methods, encouraging students to develop a more intuitive grasp of mathematical concepts. Problems and Solutions in Mathematical Olympiad ー Vol 1 (2021) specifically addresses this educational philosophy.
Integrating these techniques into your study routine, alongside resources like Holton’s guide, can significantly enhance your performance. Understanding the CMO’s emphasis on conceptual clarity and strategic thinking is crucial for tackling complex Olympiad problems effectively.
